填空题
40填空
40填空
答案解析
正确答案: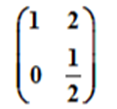
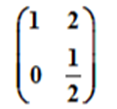
解析:
让我来帮你解析这道概率论填空题。
题目分析:
这是一个关于随机变量X的分布函数F(x)的问题。从给定的分段函数可以看出,这是一个离散型随机变量的概率分布。
详细解析:
(1) F(-2)=0
解析:当x<-1时,F(x)=0。因为-2属于这个区间,所以F(-2)=0。
理解示例:就像一个游戏,如果你还没开始玩(x<-1),你的得分肯定是0。
(2) F(0)=0.4
解析:当-1≤x<1时,F(x)=0.4。因为0在这个区间内,所以F(0)=0.4。
理解示例:相当于游戏中间的一个关卡,你达到了一定的进度,获得了40%的分数。
(3) F(1)=0.8
解析:虽然1是第二个区间的右端点,但根据分布函数的定义,应该取第三个区间的值0.8。
理解示例:就像考试成绩,达到及格线时,你会获得相应的及格分数。
(4) F(3)=1
解析:当x≥2时,F(x)=1。因为3>2,所以F(3)=1。
理解示例:游戏通关了,或者考试满分了,这就是最终结果100%。
总结:
这个分布函数描述了一个离散型随机变量,随着x的增大,累积概率逐渐增加,最后达到1。每个选项都对应着不同取值范围内的累积概率值。
希望这样的解释能帮助你更好地理解这个概率分布函数的概念!
相关题目
单选题
14判断 设随机变量X的概率密度函数为 的分布函数,则
的分布函数,则
单选题
13判断 P( )=P( )+P( )。
单选题
12判断 概率很小的事件在一次试验中几乎是不可能发生的,这个原理称为小概率事件原理。
单选题
11判断 称统计量 的无偏估计量,如果
的无偏估计量,如果 。
。
单选题
10单选 某工厂有职工400名,其中男女职工各占一半,男女职工中技术优秀的分别为20人与40人。从中任选一名职工,若已知选出的是女职工,该女职工的技术优秀的概率是( )
单选题
9单选
单选题
8单选 四人独立地投球,已知各人能投进的概率均为则有且仅有一人投进的概率为( ) 
单选题
7单选 四人独立地完成一道数学题,已知各人能完成的概率分别为  则题目不能被解出的概率为( )
则题目不能被解出的概率为( ) 
单选题
6单选 袋中有a个白球, b个黑球,从中任取一个,则取得黑球的概率是( ) 
单选题
5单选 有10件产品,其中2件次品,从中任取3件,3件全为次品的概率为( )










