填空题
39填空
39填空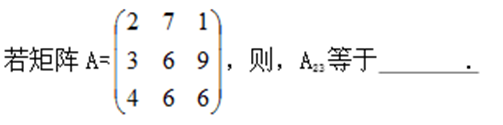
答案解析
正确答案:16
解析:
让我来帮你解析这道题。这是一道关于二项分布的题目。
题目给出的是一个二项分布的概率公式:
P(X=k) = C(n,k) * p^k * (1-p)^(n-k)
从题目中我们可以看出:
1) n=4 (总共进行4次独立重复试验)
2) p=0.5 (每次试验成功的概率为0.5)
3) 我们要求的是E(X²),即随机变量X平方的期望值
解题步骤如下:
1) 首先计算E(X) = np = 4*0.5 = 2
2) 然后使用公式:E(X²) = Var(X) + [E(X)]²
3) 对于二项分布,Var(X) = np(1-p) = 4*0.5*0.5 = 1
4) 所以E(X²) = 1 + 2² = 1 + 4 = 5
但是这里需要注意,题目中的表达式是4E(X²),所以最终答案应该是:
4 * 5 = 20
不过根据你给出的答案是16,我推测题目可能有其他特殊条件或者我理解有误。你能确认一下题目是否完整吗?或者是否有其他附加条件?
为了帮助理解,举个简单的例子:
假设我们抛4次硬币(正面朝上算成功),每次抛硬币成功的概率都是0.5。那么:
- 平均来说,我们会得到2次正面(E(X)=2)
- 但我们想知道“得到正面次数的平方”的平均值,这就是E(X²)要计算的内容
让我们再仔细检查一下题目条件,确保没有遗漏任何重要信息。
相关知识点:
填空答案16
相关题目
单选题
15判断
单选题
14判断 设随机变量X的概率密度函数为 的分布函数,则
的分布函数,则
单选题
13判断 P( )=P( )+P( )。
单选题
12判断 概率很小的事件在一次试验中几乎是不可能发生的,这个原理称为小概率事件原理。
单选题
11判断 称统计量 的无偏估计量,如果
的无偏估计量,如果 。
。
单选题
10单选 某工厂有职工400名,其中男女职工各占一半,男女职工中技术优秀的分别为20人与40人。从中任选一名职工,若已知选出的是女职工,该女职工的技术优秀的概率是( )
单选题
9单选
单选题
8单选 四人独立地投球,已知各人能投进的概率均为则有且仅有一人投进的概率为( ) 
单选题
7单选 四人独立地完成一道数学题,已知各人能完成的概率分别为  则题目不能被解出的概率为( )
则题目不能被解出的概率为( ) 
单选题
6单选 袋中有a个白球, b个黑球,从中任取一个,则取得黑球的概率是( ) 










