单选题
22单选
22单选
A
-1
B
0
C
1
D
5
答案解析
正确答案:A
解析:
让我来为你解析这道题目。
这道题考查的是随机变量的期望性质。题目给出E(X)=2, E(Y)=-3,要求E(3X-4Y-17)的值。
我们逐项分析:
A. -1 是正确答案
B. 0 不正确
C. 1 不正确
D. 5 不正确
解题步骤如下:
1) 使用期望的线性性质:E(aX+bY+c) = aE(X) + bE(Y) + c
2) 将已知条件代入:
E(3X-4Y-17) = 3E(X) - 4E(Y) - 17
= 3×2 - 4×(-3) - 17
= 6 + 12 - 17
= -1
为了帮助你理解,我举个简单的例子:
假设你有两家商店的收入情况:
- 商店X平均每天赚2元
- 商店Y平均每天亏3元
那么3家X商店减去4家Y商店再减去17元的期望值就是:
3×2 - 4×(-3) - 17 = -1元
因此正确答案是A.-1。
这个结果告诉我们,在概率论中,期望具有很好的线性性质,即使对于线性组合的随机变量,我们也可以直接用线性运算求出期望值。
相关知识点:
试题19可逆矩阵选B
相关题目
单选题
7单选 已知随机变量X服从[1, 5]上的均匀分布,则D ( )=( )
单选题
6单选 设A,B为随机事件,且P( )=0.7,P( )=0.4,则 
单选题
5单选 设随机变量X服从[0,2]上的均匀分布,Y=2X+1,则D( )=( )
单选题
4单选 设随机变量X服从参数为2的泊松分布,且Y =2X -3, 则E( )=( )
单选题
3单选 设离散型随机变量的概率分布为 
单选题
2单选 若随机事件A与B相互独立,则P( )=( )
单选题
1单选题 设A,B为随机事件,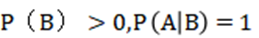 则必有( )
则必有( )
单选题
25计算题 设连续型随机变量X的分布函数为 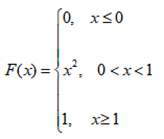 。求:(1)X的概率密度f(x);(2)X落在区间(0.2,0.8)的概率。
。求:(1)X的概率密度f(x);(2)X落在区间(0.2,0.8)的概率。
单选题
24计算题 设连续型随机变量X的分布函数为 。求: (1)系数k; (2)P(0.25
(1)系数k; (2)P(0.25
单选题
23计算题 设二维随机变量(X,Y)的联合分布列为










