相关题目
4.函数y =  sin x
sin x  在x = 0 处的导数是( )。
在x = 0 处的导数是( )。
2.函数g = f ( ) 在点x0 处的左导数f'一(x0 ) 和右导数f (x0 ) 存且相等是f ( ) 在点x0
(x0 ) 存且相等是f ( ) 在点x0
可导的( )。
1.以下说法成立的是( )。
2.利用极限存在准则证明: lnnull n( 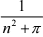 +
+ 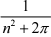 + . . . +
+ . . . +  )= 1 。 证:设xn = n
)= 1 。 证:设xn = n
 +
+ 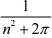 + . . . +
+ . . . + 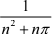 ))| ,
))| ,
yn = n
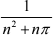 +
+  + . . . +
+ . . . + 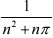 ))| =
))| = 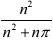 ,
,
zn = n
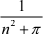 +
+  + . . . +
+ . . . +  ))| =
))| =  ,
,n)w n)w
所以,由夹逼定理可知lim xn = 1,
证毕。
1.证明:方程x 5 - 3x = 1在区间(1,2) 内至少有一个根。
证:设函数f (x) = x 5 - 3x - 1,因其定义域为( - w,+ w ), 则f (x) 在闭区间[1,2] 上连续, 又因为f (1) = 15 - 3〉1 - 1 = -3 想 0 ,而f (2) = 25 - 3〉2 - 1 = 25 > 0 ,则 根据零点定理, 在(1,2) 内至少有一点 ,使得f(
,使得f( ) = 0 ,即
) = 0 ,即 5 - 3
5 - 3 - 1 = 0 ,其 中1 想
- 1 = 0 ,其 中1 想 想 2 ,也即方程x 5 - 3x = 1在区间(1,2) 内至少有一个根是
想 2 ,也即方程x 5 - 3x = 1在区间(1,2) 内至少有一个根是 ,证毕。
,证毕。
18.已知函数f (x) =〈|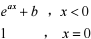 ,讨论a 、b 为何值时, f (x) 在x = 0 处连续。
,讨论a 、b 为何值时, f (x) 在x = 0 处连续。|(a sin x) - b ,x > 0
解: lim-(eax + b) = b = f (0) = 1 不 b = 1,
lx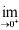 (
(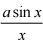 - b) = a - b = f (0) = 1 不 a = 2 。
- b) = a - b = f (0) = 1 不 a = 2 。
17.设函数f (x) =〈 ,应当怎样选择a ,使得f (x) 成为在(-的,+的) 内
,应当怎样选择a ,使得f (x) 成为在(-的,+的) 内
的连续函数。解: lim- ex = 1 = f (0) = a 不 a = 1。
(
16.设函数f (x) =〈| x - 1 , x 丰 1 是其定义域上的连续函数,求k 的值。 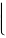 2k - 3 , x = 1
2k - 3 , x = 1
解: lixnull = lixnull(x2 + x + 1) = 3 = f (1) = 2k - 3 不 k = 3 。
= lixnull(x2 + x + 1) = 3 = f (1) = 2k - 3 不 k = 3 。
13.计算极限lxnull( 2xnullnull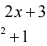 ) 。
) 。2 一 +
解:上式分子分母同除x2 , 则有原式 = lim x x = 。
x )w 4 + 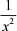 2
214.计算极限lim(| ( x 一 1))|x
解:原式= lxnull null2 ))|x = lxnull
null2 ))|x = lxnull 1+
1+  一
一 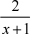 ))|
))| x
x= lxnull
 1 +
1 +  -
- 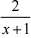 ))|
))|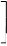 -
-  = e-2 。
= e-2 。x)0 x sin x
解:当x ) 0 时有1- cos x ~  x2 , sin x ~ x ,
x2 , sin x ~ x ,所以,原式= lim
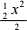 = ( 1)
= ( 1)
。
( (x3 - 1)
12.计算极限lixnull (2xxnull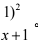
解:原式= lixnull (2xxnull
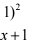 =
= 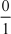 = 0
= 0




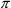 ( )。
( )。
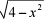 - x、 - 2
- x、 - 2 





