相关题目
20.应用对数求导法求函数y = xsin x 。
解:方程两边取对数得:
lny = sin x . lnx
上式两边对x 求导得: . yp = cos x . lnx + sin x .
. yp = cos x . lnx + sin x . 
所以
yp = y(cos x . Inx +  )
)
= xsin x (cos x . Inx + 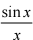 )
)
19.求由参数方程〈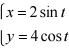 所确定的函数在t = null 处的切线方程。
所确定的函数在t = null 处的切线方程。
解:由( )
(dy ) ( dt ) ( 一 2 sin t)
dx = (dx) = cos t
当t = (d几4t)时,x = 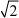 ,y = 2
,y = 2 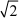 ,
,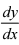 = 一2.
= 一2.
所以函数的切线方程为:
y = 一2x + 4 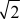 .
.
18.求曲线y = x + ex 在点x = 0 处的切线方程。
解: y, = 1 + ex ,y,( ) = 2 ,曲线过(0,1) ,由点斜式知,
曲线y = x + ex 在点x = 0 处的切线方程为y = 2x + 1 .
17.求复合函数y = (1+ x2 ) arctan x 的导数。
解:因
y, = (1+ x2 ), arctan x + (1+ x2 )(arctan x),
= 2x arctan x + 1
16.求复合函数y = cos8x 的导数。
解:因
y, = (cos8x),
= 一 sin 8x . (8x),
= 一8 sin 8x
15.求复合函数f ( ) = cos3 3x + e3x 的导数。
解: f  ( ) = (cos3 3x + e3x )
( ) = (cos3 3x + e3x ) 
= 一9 cos2 3x sin 3x + 3e3x
14.求由参数方程〈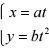 所确定的函数的导数
所确定的函数的导数 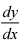 。
。
解: 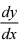 =
= 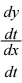 =
= 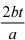
13.求由方程ey + xy 一 e = 0 所确定的隐函数y = f ( ) 的导数。
解:方程两边分别对x 求导,得ey 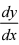 + y + x .
+ y + x . 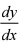 = 0
= 0
由此得 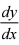 = 一
= 一  (x + ey
(x + ey  0)
0)
12.求由方程x 一y +  siny = 0 所确定的隐含数y = f ( ) 的导数。
siny = 0 所确定的隐含数y = f ( ) 的导数。
解:方程两边分别对x 求导,得1 - 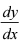 +
+  cos y .
cos y . 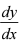 = 0
= 0
由此得 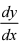 = 2 一 nullos y
= 2 一 nullos y
11.设函数y = x 3 + 4x ,求 dy。
解:因dy = d (x3 + 4x) = (x3 + 4x)  dx = (3x2 + 4)dx
dx = (3x2 + 4)dx
所以dy = (3x2 + 4)dx




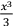 +C】 。
+C】 。






