相关题目
2.求定积分j14 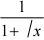 dx
dx
解:令  = t ,则 x = t2 ,dx = 2tdt .x = 1 不 t = 1, x = 4 不 t = 2
= t ,则 x = t2 ,dx = 2tdt .x = 1 不 t = 1, x = 4 不 t = 2
原式=2j12 dt -( 2)j12 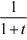 dt =2 - 2[ln(1 + t)]null =2 + 2 ln
dt =2 - 2[ln(1 + t)]null =2 + 2 ln 

1.求定积分j-31 (4x - x2 )dx
解:j-31 (4x - x2 )dx =  2x2 -
2x2 - 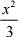
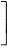 3-1
3-1
= (2 根 32 -  ) - (2 +
) - (2 +  )
)
= 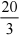
14. ( )积分值仅与被积函数及积分区间有关,与积分变量的字母无关。 15. ( ) 函数f ( ) 在[a,b]上有定义且 f ( )
( )  在[a,b]上可积,此时积分
在[a,b]上可积,此时积分
jab f ( )dx 必存在。
13. ( ) j-aa x[f ( ) + f ( )]dx = 0 。
12. ( ) 若f ( ) 在[a, b]上可积,则f ( ) 在[a, b]上有界。
9. ( ) 若f ( ), g( ) 均可积,且f ( ) < g( ) ,则 jbaf ( )dx < jbag( )dx 。 10. ( ) 若f ( ) 在[a, b]上连续,且jbaf 2 ( )dx = 0 ,则在 [a, b]上f ( ) = 0 。 11. ( ) 若[c, d ] 仁 [a, b] ,则 jcd f ( )dx < jbaf ( )dx 。
8. ( ) 定积分的值是一个确定的常数。
7. ( ) j-
 x 2 sin 2xdx = 2j0
x 2 sin 2xdx = 2j0 x 2 sin 2xdx 。
x 2 sin 2xdx 。
6. ( ) 设j-11 f ( )dx = -1,则 j1- 1 2f ( )dx = 2。
5. ( ) 设a < b ,则积分jab (x - x2 )dx 取得最大值时, a = 0, b = 1 。




 (1+ n)n = e 。
(1+ n)n = e 。






