6.计算y = x + e一 x sin x 的二阶导数。
解: y = 1 一 e一x sin x + e一x cos x
y = e一x sin x 一 e一x cos x 一 e一x cos x 一 e一x sin x = 一 2e一x cos x

3.计算不定积分∫ 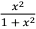dx。
解:原式 = ∫ 1− 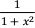dx (3 分)
= x −aTctan x + C。 (3 分)

2.计算不定积分∫ (2x2 −3 cos x + 1)dx。
解:原式 = 2∫ x2 dx−3∫ cos xdx + ∫ 1dx (3 分)
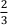= x3 − 3sin x +x + C 。 (3 分)

1.求∫ x2 xdx。
解:原式 = ∫ xdx (3 分)
2 ( 7)

10.∫ [f( ) + g( )]dx = ∫ f( )dx + ∫ g( )dx。( )

9.cos x的不定积分是sinx。( )

8.sin x的不定积分是−cos x。( )

7.不定积分∫ xa dx = axa−1 +C ,( )。( )

6.函数的原函数若存在则必有无数个。( )

5.∫ |x|dx = 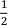x2 +C 。 ( )

1.在区间 I 上,函数f( )的一个原函数称为函数f( )在区间 I 上的不定积分。( ) 2.任何函数都存在原函数。( ) 3.若函数f( )在( )上连续,则f( )在( )上有原函数。 ( ) 4.若函数f( )在( )上有界,则f( )在( )上有原函数。 ( )