相关题目
1.若j01 (2x + k )dx = 2 ,则k = ( ) .
18.计算积分∫ xex dx。解: ∫ xe dxx = ∫ xdex = xe −x ∫ ex dx
= ex (x 1)− + C。
17.计算不定积分∫ tet2dt。解: ∫ tet2 dt =
 ∫ et2 dt2
∫ et2 dt2
=  et2 + C。
et2 + C。
9.计算不定积分∫  dx。
dx。
解: ∫  dx = 3 ×
dx = 3 × 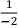 ∫
∫  d(1−2x)
d(1−2x)
(3 分)=
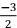 ln|1−2x| + C。
ln|1−2x| + C。
= aTctan ex +C。
8.求不定积分∫ cos2  dx。
dx。
解:原式 = ∫  dx (3 分)
dx (3 分)
= 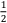 (x + sin x) + C 。 (3 分)
(x + sin x) + C 。 (3 分)
7.计算不定积分∫ 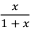 dx。
dx。
解:原式 = ∫ 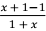 dx (2 分)
dx (2 分)
= ∫ dx − ∫ 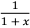 dx (2 分)
dx (2 分)
= x−ln|x + 1 | + C 。 (2 分)
6.求∫ (ex + 3 cos x )dx。
解: ∫ (ex + 3 cos x )dx = ∫ ex dx + ∫ 3 cos x dx (3 分)
= ex +3sin x +C 。 (3 分)
5.求∫ (x3 + 5 cos x + 1)dx。
解:原式 = ∫ x3 dx + 5 ∫ cos x dx + ∫ dx (3 分)
=  x4 +5sin x +x + C 。 (3 分)
x4 +5sin x +x + C 。 (3 分)
4.计算不定积分∫ 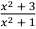 dx。
dx。
解:原式 = ∫ 1 + 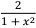 dx (3 分)
dx (3 分)
= x + 2aTctanx + C 。 (3 分)
3.计算不定积分∫ 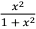 dx。
dx。
解:原式 = ∫ 1− 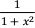 dx (3 分)
dx (3 分)
= x −aTctan x + C。 (3 分)




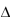 x = 0.01时的微分为 0.02 。 ( )
x = 0.01时的微分为 0.02 。 ( )






