单选题
19.函数y=3x+5,x∈R的反函数是().
A
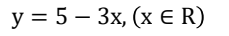
B

C
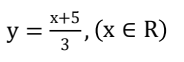
D

答案解析
正确答案:B
解析:
首先,我们知道函数y=3x+5的反函数可以通过将x和y互换位置来得到。也就是说,我们需要解出x关于y的表达式。
首先,将y=3x+5改写为x=(y-5)/3。这样,我们就得到了反函数x=(y-5)/3。
所以,答案是B.  。
如果你想更直观地理解反函数的概念,可以想象一下你在一个游乐园的迷宫中迷路了,而反函数就像是一张地图,帮助你找到回到出口的路线。反函数就是将原函数的输入和输出进行对调,帮助我们从输出值反推回输入值的过程。希望这个比喻能帮助你更好地理解反函数的概念。如果有任何疑问,欢迎继续提问哦!
。
如果你想更直观地理解反函数的概念,可以想象一下你在一个游乐园的迷宫中迷路了,而反函数就像是一张地图,帮助你找到回到出口的路线。反函数就是将原函数的输入和输出进行对调,帮助我们从输出值反推回输入值的过程。希望这个比喻能帮助你更好地理解反函数的概念。如果有任何疑问,欢迎继续提问哦!
 。
如果你想更直观地理解反函数的概念,可以想象一下你在一个游乐园的迷宫中迷路了,而反函数就像是一张地图,帮助你找到回到出口的路线。反函数就是将原函数的输入和输出进行对调,帮助我们从输出值反推回输入值的过程。希望这个比喻能帮助你更好地理解反函数的概念。如果有任何疑问,欢迎继续提问哦!
。
如果你想更直观地理解反函数的概念,可以想象一下你在一个游乐园的迷宫中迷路了,而反函数就像是一张地图,帮助你找到回到出口的路线。反函数就是将原函数的输入和输出进行对调,帮助我们从输出值反推回输入值的过程。希望这个比喻能帮助你更好地理解反函数的概念。如果有任何疑问,欢迎继续提问哦!相关题目
单选题
181、Word具有自动保存文件的功能。( )(1.0)
单选题
180、在Word中不能画图,只能插入外部图片。( )(1.0)
单选题
179、删除桌面应用程序的快捷方式图标,就是删除了对应的应用程序文件。( )(1.0)
单选题
178、在Word中,进行文档的页面设置可以在“开始”选项卡的“页面设置”组中进行。( )(1.0)
单选题
177、在Word中,单击“保存”命令就是保存当前正在编辑的文档,若是第一次保存,则会打开“另存为”对话框。( )(1.0)
单选题
176、在Word编辑状态下,若对所选的某一段执行了“删除”(或按Delete键)操作,则该段落将被移到回收站内。( )(1.0)
单选题
175、在Word编辑状态下,将文档中的某段文字误删除之后将无法恢复。( )(1.0)
单选题
174、在Word的字符格式化中,可以把选定的文本设置成上标或下标的效果。( )(1.0)
单选题
173、在Word中设置段落格式时,不能同时设置多个段落的格式。( )(1.0)
单选题
172、关闭电脑后,剪贴板中内容会丢失。( )(1.0)










