单选题
5.如果f( ) = 2x,那么函数f( )的不定积分可表示为( )。
A
x2
B
x2 +1
C
x2 −1
D
x2 + C
答案解析
正确答案:XD
解析:
好的!让我们一起来解决这个单选题。
题目:如果 \( f(x) = 2x \),那么函数 \( f(x) \) 的不定积分可以表示为( )。
首先,我们需要理解什么是“不定积分”。不定积分是求一个函数的原函数的过程。简单来说,如果我们有一个函数 \( f(x) \),那么它的不定积分就是找到一个函数 \( F(x) \),使得 \( F'(x) = f(x) \)。此外,不定积分的结果会包含一个任意常数 \( C \),因为任何常数的导数都是0。
对于本题:
- 已知 \( f(x) = 2x \)。
- 我们需要找到一个函数 \( F(x) \),使得 \( F'(x) = 2x \)。
接下来,我们来求 \( 2x \) 的原函数:
\[ \int 2x \, dx \]
根据积分的基本公式:
\[ \int x^n \, dx = \frac{x^{n+1}}{n+1} + C \]
对于 \( n = 1 \):
\[ \int 2x \, dx = 2 \int x \, dx = 2 \left( \frac{x^2}{2} \right) + C = x^2 + C \]
因此,\( f(x) = 2x \) 的不定积分是 \( x^2 + C \)。
选项分析:
- A: \( x^2 \) (缺少常数项)
- B: \( x^2 + 1 \) (虽然形式上对,但不适用于所有情况)
- C: \( x^2 - 1 \) (缺少常数项)
- D: \( x^2 + C \) (正确)
所以,正确答案是 **D: \( x^2 + C \)**。
为了加深理解,我们可以用一个生动的例子来说明:
假设你在开车,速度表显示你的速度是 \( 2x \) 米/秒(其中 \( x \) 是时间)。那么你的位置(即路程)随着时间的变化关系应该是 \( x^2 + C \) 米,这里的 \( C \) 可以看作是你开始计时的位置偏移量。
相关题目
单选题
12.设f( ) ,g( )在I上的原函数分别是F( )和G( ),则在I上有( )。
单选题
11.下列不定积分中不适合用分部积分计算的是( )。
单选题
10.当u( ) = ( )时,可用第一类换元积分法计算不定积分∫ 2xeu( ) dx。
单选题
9.下列函数中( )是x2 的一个原函数,并且y(1) = 3。
单选题
8.若∫ f( )dx = e −x + C ,则f′ ( ) = ( )。
单选题
7.幂函数的原函数一定是( )。
单选题
6.设f( ) = ex ,则 ∫ 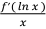 dx = ( )。
dx = ( )。A. x + C
B. ln x +C
单选题
5.如果f( ) = 2x,那么函数f( )的不定积分可表示为( )。
单选题
4.如果f( ) = cosx,那么函数f( )的不定积分可表示为( )。
单选题
3.如果f( ) = sinx,那么函数f( )的不定积分可表示为( )。










