单选题
4.如果f( ) = cosx,那么函数f( )的不定积分可表示为( )。
A
sinx
B
−cosx + C
C
cosx + C
D
sinx + C
答案解析
正确答案:XD
解析:
好的,让我们一起来解析这道题。
题目要求我们找到函数 \( f(x) = \cos x \) 的不定积分表达式。
首先,我们需要回顾一下基本的微积分知识:
- 不定积分是求原函数的过程。
- 对于一个函数 \( f(x) \),其不定积分可以表示为 \( \int f(x) \, dx \)。
现在具体来看题目中的函数 \( f(x) = \cos x \):
- 我们需要找出一个函数 \( F(x) \),使得 \( F'(x) = \cos x \)。
根据导数的基本公式,我们知道:
\[ \frac{d}{dx} (\sin x) = \cos x \]
因此,\( \sin x \) 是 \( \cos x \) 的一个原函数。但是,由于不定积分包含常数项 \( C \),所以完整的不定积分表达式为:
\[ \int \cos x \, dx = \sin x + C \]
接下来我们来看选项:
- A: sinx (缺少常数项 \( C \))
- B: −cosx + C (这里 \( -\cos x \) 的导数不是 \( \cos x \))
- C: cosx + C (这里 \( \cos x \) 的导数是 \( -\sin x \))
- D: sinx + C (正确)
综上所述,正确答案是 **D: sinx + C**。
为了更生动地理解这一点,我们可以类比生活中的例子:假设你每天记录走路的步数,而步数是时间的函数。如果你想知道一段时间内总共走了多少步,你需要对每一步进行累加,这个过程就像求不定积分一样。在这个过程中,每一步的累积总和加上起始点的位置(相当于常数项 \( C \)),才能得到最终的总步数。
相关题目
单选题
1.f( )的两个原函数之间相差【任意常数】。
单选题
12.设f( ) ,g( )在I上的原函数分别是F( )和G( ),则在I上有( )。
单选题
11.下列不定积分中不适合用分部积分计算的是( )。
单选题
10.当u( ) = ( )时,可用第一类换元积分法计算不定积分∫ 2xeu( ) dx。
单选题
9.下列函数中( )是x2 的一个原函数,并且y(1) = 3。
单选题
8.若∫ f( )dx = e −x + C ,则f′ ( ) = ( )。
单选题
7.幂函数的原函数一定是( )。
单选题
6.设f( ) = ex ,则 ∫ 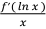 dx = ( )。
dx = ( )。A. x + C
B. ln x +C
单选题
5.如果f( ) = 2x,那么函数f( )的不定积分可表示为( )。
单选题
4.如果f( ) = cosx,那么函数f( )的不定积分可表示为( )。










