判断题
31判断 零向量不是任何一组向量的线性组合。
A
正确
B
错误
答案解析
正确答案:B
解析:
让我来为你解析这道题。
这道题的正确答案是“错误”,原因如下:
1. 零向量可以表示为任何一组向量的线性组合,只要所有系数都取0。具体来说:
- 设有向量组α₁, α₂, ..., αn
- 则 0·α₁ + 0·α₂ + ... + 0·αn = 0(零向量)
2. 示例说明:
- 比如在二维空间中,对于向量(1,0)和(0,1)
- 我们可以写成:0*(1,0) + 0*(0,1) = (0,0)
- 这就是用这两个向量表示零向量
3. 特别注意:
- 零向量本身就是一个特殊的向量
- 它可以被任何向量组线性表示
- 这种表示方式是唯一的,即所有系数都为0
因此,说“零向量不是任何一组向量的线性组合”是不正确的。实际上,零向量总是可以被任何向量组线性表示的,只是系数全部为0而已。
这个结论在向量空间理论中非常重要,它体现了零向量的独特性质,在许多定理证明和实际应用中都会用到。
相关知识点:
零向量线性组合判断
相关题目
单选题
23计算题 设二维随机变量(X,Y)的联合分布列为
单选题
22计算题 设有甲、乙两袋,甲袋中装有n只白球、m只红球;乙袋中装有N只白球、M只红球。今从甲袋中任意取一只球放入乙袋中,再从乙袋中任意取一只球。求从乙袋中取到白球的概率。
单选题
21计算题 甲乙两人独立解某一道数学题,已知该题被甲独立解出的概率为0.6,被甲或乙解出的概率为0.92. (1)求该题被乙独立解出的概率; (2)求解出该题的人数。
单选题
20填空 设随机变量X的概率密度是 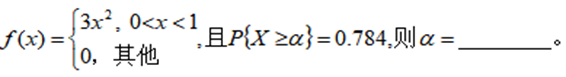
单选题
19填空 利用正态分布的结论,有 
单选题
18填空 设A、B为两个随机事件,若P( )=0.4,P( )=0.3, 
单选题
17填空 已知随机向量( )的联合概率密度 
单选题
16填空 设离散型随机变量X的分布函数为:
单选题
15判断
单选题
14判断 设随机变量X的概率密度函数为 的分布函数,则
的分布函数,则










