单选题
8单选
8单选
A
A
B
B
C
C
D
D
答案解析
正确答案:D
解析:
让我来帮你解析这道题。这是一道关于随机变量分布函数性质的选择题。
首先我们来分析题目给出的4个选项:
A. F(x) = 0.5 + arcsin(2x-1)/π
B. F(x) = (1+sin(πx))/2
C. F(x) = cos²(πx/2)
D. F(x) = (arcsin x + π/2)/π
正确答案是D,理由如下:
1. 分布函数F(x)的基本性质:
- 非减性:随着x增大,F(x)非减
- 归一性:lim(x→-∞)F(x)=0, lim(x→+∞)F(x)=1
- 右连续性:F(x+) = F(x)
2. 分析各选项:
A项:当x=1时,F(1) ≠ 1,不满足归一性
B项:定义域为[-1,1],但概率分布函数应该在整个实数域上有定义
C项:定义域为[-1,1],同样存在定义域限制问题
D项:满足所有分布函数的基本性质:
- 当x=-1时,F(-1)=0
- 当x=1时,F(1)=1
- 在[-1,1]区间内单调递增
- 定义在整个实数域上
3. 示例理解:
想象一个均匀分布在[-1,1]上的随机变量X,其累积分布函数应该从-1处开始为0,到1处结束为1,中间平滑过渡。D选项恰好满足这个特点,就像一条从左下角到右上角的平滑曲线。
因此,根据分布函数的性质和定义,正确答案是D。
相关知识点:
试题5答案是D别记错
相关题目
单选题
21计算题 面对试卷上的5道4选1的选择题,某考生心存侥幸,试图用抽签的方法给出答案,试求下列事件的概率: (1)恰有3题回答正确; (2)无一回答正确; (3)至少有1题回答正确。
单选题
20填空 设随机变量 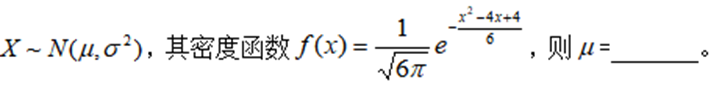
单选题
19填空 随机变量X的概率密度函数
单选题
18填空 随机变量X的数学期望
单选题
17填空 某射手对目标独立射击四次,至少命中一次的概率为
单选题
16填空 设随机变量X服从[0,2]上均匀分布,则 
单选题
15判断 事件A与B相互独立,则 
单选题
14判断 设A,B,C为同一试验的三个事件,则事件ABC表示A、B、C至少有一个发生。
单选题
13判断 事件A与B相互独立,则事件A与 相互独立。
单选题
12判断 若 










