单选题
7.已知f ( ) 为偶函数,且j02 f ( )dx =
7.已知f ( ) 为偶函数,且j02 f ( )dx =  ,则定积分 j-22 f ( )dx = ( )
,则定积分 j-22 f ( )dx = ( )
A
0
B
-1
C
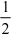
D
1
答案解析
正确答案:XD
解析:
好的,让我们一起来解析这道题目。
题目给出的信息是:\( f(x) \) 是一个偶函数,并且 \( \int_0^2 f(x) \, dx = 1 \)。我们需要求 \( \int_{-2}^2 f(x) \, dx \) 的值。
### 偶函数的性质
首先,我们需要理解偶函数的定义:如果一个函数满足 \( f(-x) = f(x) \),那么这个函数就是偶函数。例如,\( f(x) = x^2 \) 就是一个偶函数。
### 定积分的几何意义
对于偶函数 \( f(x) \),在对称区间 \([-a, a]\) 上的定积分可以分成两部分:
\[ \int_{-a}^a f(x) \, dx = \int_{-a}^0 f(x) \, dx + \int_0^a f(x) \, dx \]
由于 \( f(x) \) 是偶函数,所以 \( f(-x) = f(x) \),因此:
\[ \int_{-a}^0 f(x) \, dx = \int_0^a f(-x) \, dx = \int_0^a f(x) \, dx \]
也就是说,在对称区间 \([-a, a]\) 上,定积分可以简化为:
\[ \int_{-a}^a f(x) \, dx = 2 \int_0^a f(x) \, dx \]
### 应用到本题
题目中给出的是 \( \int_0^2 f(x) \, dx = 1 \),根据上述性质,我们可以计算 \( \int_{-2}^2 f(x) \, dx \):
\[ \int_{-2}^2 f(x) \, dx = 2 \int_0^2 f(x) \, dx = 2 \cdot 1 = 2 \]
因此,正确答案是 D: 2。
希望这个解释对你有所帮助!
相关题目
单选题
10.曲线y = sin x 在点x = 几 处的切线方程是( )。
单选题
9.反函数的导数等于直接函数导数的( )。
单选题
8.二阶及二阶以上的导数统称为( )。
单选题
7. 如 果 u, v 都 是 x 的 可 导 函 数 , 则 y = uv 也 是 x 的 可 导 函 数 , 那 么 ( ), = ( )
单选题
6.函数f ( ) = xex 的二阶导数为: ___( ___。
单选题
5. d ( n xdx 。
单选题
4. 函数f ( ) 在x0 处的导数f ' ( ) 的几何意义是( )
单选题
3.函数f ( ) 在点x0 连续是f ( ) 在x0 可导的( ) 条件。
单选题
2.设lx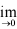
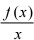 = k, f ( ) = 0, 则f
= k, f ( ) = 0, 则f  ( ) =( )_。
( ) =( )_。
单选题
1.函数f ( ) = x3 在x = 1 , 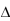 x = -0.03 时的微分为( )。
x = -0.03 时的微分为( )。










