简答题
2.设函数f (x) = x 3 + 1 ,求 f (x 2 ) 。
2.设函数f (x) = x 3 + 1 ,求 f (x 2 ) 。
解: f (x 2 ) = (x 2 )3 + 1 = x 6 + 1。
 3.设函数f (x) =
3.设函数f (x) =  求f
求f  f [f (x)]} 。
f [f (x)]} 。
解: f [f (x)] = 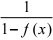 =
=  =
=  =
=  ,
,
f  f [f (x)]} =
f [f (x)]} =  =
=  ( )
( ) ( 1) = x
( 1) = x
 1
1 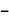 x
x
 4.计算极限lx
4.计算极限lx

解:原式=  =0。
=0。
 5.计算极限lim( x2 )
5.计算极限lim( x2 )
。
 x
x 
 x
x
 x
x 
 x + 1
x + 1

 6.计算极限lim
6.计算极限lim
。
 (sin ax)
(sin ax)
x  0 ax
0 ax
。
 x
x 
 x x
x x
。
 x
x 
 x
x 
 x x
x x 
 x
x
。
 8.计算极限lim
8.计算极限lim
。
解:当x  0 时有sin 2x ~ 2x, sin 3x ~ 3x ,
0 时有sin 2x ~ 2x, sin 3x ~ 3x ,
 所以,原式=lim ( 2x) = ( 2)
所以,原式=lim ( 2x) = ( 2)
。
 9.计算极限lim(1 一 ( 1 ) )3x
9.计算极限lim(1 一 ( 1 ) )3x
。
 x)w x
x)w x
。
答案解析
正确答案:空
相关题目
单选题
7. ( ) j-
 x 2 sin 2xdx = 2j0
x 2 sin 2xdx = 2j0 x 2 sin 2xdx 。
x 2 sin 2xdx 。
单选题
6. ( ) 设j-11 f ( )dx = -1,则 j1- 1 2f ( )dx = 2。
单选题
5. ( ) 设a < b ,则积分jab (x - x2 )dx 取得最大值时, a = 0, b = 1 。
单选题
4. ( ) 定积分的几何意义是相应曲边梯形的面积之和。
单选题
3. ( ) 若函数f ( ) 在(a,b)上连续,则 f ( ) 在(a,b)上可积。
单选题
2. ( ) 若函数f ( ) 在(a,b)上有界,则 f ( ) 在(a,b)上可积。
单选题
1. ( ) 若函数f ( ) 在[a,b]上连续,则f ( ) 在[a,b]上可积。
单选题
20.jab f ( )dx + jba f ( )dx = ( )。
单选题
18.若函数f ( ) = 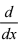 j0x sin( )dt ,则 f ( ) = ( ) 。 19.已知f ,( )j02 f ( )dx = 50 ,且 f ( ) = 0 ,则 f ( ) =( )。
j0x sin( )dt ,则 f ( ) = ( ) 。 19.已知f ,( )j02 f ( )dx = 50 ,且 f ( ) = 0 ,则 f ( ) =( )。
单选题
17.若函数F( ) = j1x ( )dt( ) 的单调递减区间为 ( 。










