相关题目
8.计算j01 e 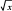 dx .
dx .
解:先用换元法:令 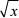 = t ,则 x = t2 ,dx = 2tdt ,且
= t ,则 x = t2 ,dx = 2tdt ,且
当x = 0 时, t = 0 ;当 x = 1 时, t = 1 .
换元后分部积分, j01 e 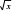 dx = 2j01 tet dt = 2j01 td(et )= 2([tet ]null - j01 et dt)
dx = 2j01 tet dt = 2j01 td(et )= 2([tet ]null - j01 et dt)
= 2(e - [et ] )null = 2[e - (e - 1)]= 2
3 6
7.求定积分j12  (1 +
(1 +  )dx .
)dx .
解: j12 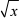 (1 +
(1 + 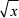 )dx = j12 (
)dx = j12 ( 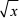 + x)dx
+ x)dx
「 ( 3 ) ]2 = |
= | +
+  |
|
= +
1
= 3
6. 求定积分j1+的 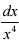 的值. 解: j1+的
的值. 解: j1+的 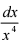 =
= 
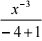
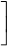
 的
的
10
= 3
5.求定积分j12 (x2 + 1)dx
解: j12 (x2 + 1)dx = 
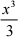 + x
+ x 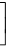 null
null(8 ) ( 1)
4.求定积分j02 cos 2xdx
解:原式= 
 j02 cos 2xd 2x
j02 cos 2xd 2x
=  [sin 2x]
[sin 2x]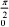
=0
3.求定积分j04 cos2 xdx
解:原式=  j04
j04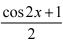 dx
dx
=  j04
j04 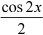 dx +
dx +  j04
j04 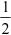 dx
dx
=  +
+ 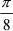

2.求定积分j14 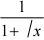 dx
dx
解:令  = t ,则 x = t2 ,dx = 2tdt .x = 1 不 t = 1, x = 4 不 t = 2
= t ,则 x = t2 ,dx = 2tdt .x = 1 不 t = 1, x = 4 不 t = 2
原式=2j12 dt -( 2)j12 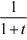 dt =2 - 2[ln(1 + t)]null =2 + 2 ln
dt =2 - 2[ln(1 + t)]null =2 + 2 ln 





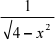 的定义域是( 2 < x < 2 )。
的定义域是( 2 < x < 2 )。






