判断题
29判断
29判断
A
正确
B
错误
答案解析
正确答案:B
解析:
让我来帮你分析这道判断题。题目表述的是“若A与B互不相容,则A的对立事件与B的对立事件也互不相容”。
这个判断是错误的,我来解释原因:
1) 首先明确概念:
- 互不相容(互斥):两个事件不能同时发生
- 对立事件:一个事件发生与否的两种情况
2) 分析过程:
设A和B互不相容,即P(AB)=0
那么A的对立事件为A̅,B的对立事件为B̅
根据概率论知识:
P(A̅∩B̅) = P[(A∪B)'] = 1 - P(A∪B)
3) 反例说明:
举个简单例子:
假设我们掷一个骰子
令A={出现1点}
令B={出现2点}
显然A和B互不相容
但A̅={出现2,3,4,5,6点}
B̅={出现1,3,4,5,6点}
此时A̅和B̅是可以同时发生的(比如出现3、4、5或6点)
因此,原命题是错误的。两个互不相容事件的对立事件可以同时发生,也就是说它们不是互不相容的。
这就是为什么答案选择“错误”的原因。希望这个解释能帮助你理解这个概率论概念。
相关题目
单选题
25计算题 设连续型随机变量X的分布函数为 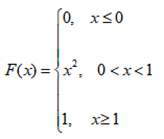 。求:(1)X的概率密度f(x);(2)X落在区间(0.2,0.8)的概率。
。求:(1)X的概率密度f(x);(2)X落在区间(0.2,0.8)的概率。
单选题
24计算题 设连续型随机变量X的分布函数为 。求: (1)系数k; (2)P(0.25
(1)系数k; (2)P(0.25
单选题
23计算题 设二维随机变量(X,Y)的联合分布列为
单选题
22计算题 设有甲、乙两袋,甲袋中装有n只白球、m只红球;乙袋中装有N只白球、M只红球。今从甲袋中任意取一只球放入乙袋中,再从乙袋中任意取一只球。求从乙袋中取到白球的概率。
单选题
21计算题 甲乙两人独立解某一道数学题,已知该题被甲独立解出的概率为0.6,被甲或乙解出的概率为0.92. (1)求该题被乙独立解出的概率; (2)求解出该题的人数。
单选题
20填空 设随机变量X的概率密度是 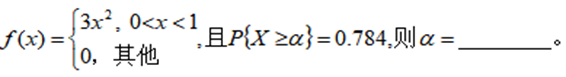
单选题
19填空 利用正态分布的结论,有 
单选题
18填空 设A、B为两个随机事件,若P( )=0.4,P( )=0.3, 
单选题
17填空 已知随机向量( )的联合概率密度 
单选题
16填空 设离散型随机变量X的分布函数为:










