单选题
6单选 矩阵A的不同特征值对应的特征向量().
A
线性相关的
B
线性无关的
C
无法判断他们的相关性
D
正交
答案解析
正确答案:B
解析:
让我来为你解析这道题。
题目分析:
这道题考查的是特征值与特征向量之间的关系,特别是不同特征值对应的特征向量的线性相关性。
选项分析:
A. 线性相关的 - 错误
这是不正确的。不同特征值对应的特征向量不可能线性相关。
B. 线性无关的 - 正确
这是正确答案。根据线性代数的基本定理,属于不同特征值的特征向量必定线性无关。
C. 无法判断他们的相关性 - 错误
我们是可以明确判断的,它们一定是线性无关的。
D. 正交 - 错误
虽然在某些特殊情况下(如对称矩阵),不同特征值对应的特征向量可能正交,但这不是普遍规律,因此不能作为一般结论。
简单示例:
假设我们有一个2×2矩阵A,它有两个不同的特征值λ₁和λ₂。
- λ₁对应的特征向量为v₁ = [1,0]ᵀ
- λ₂对应的特征向量为v₂ = [0,1]ᵀ
这两个特征向量显然线性无关,因为不存在常数k使得v₁ = kv₂。
选择B的原因:
这是线性代数中的一个基本定理:如果λ₁ ≠ λ₂,则对应于λ₁的特征向量v₁和对应于λ₂的特征向量v₂必定线性无关。这个性质对于任何方阵都成立,是特征值理论的重要基础。
相关知识点:
试题3特征向量相关性
相关题目
单选题
23计算题 设连续型随机变量X的概率密度为:  ,
, 。
。
单选题
22计算题 设A,B为随机事件,且P(B)>0.证明:  。
。
单选题
21计算题 面对试卷上的5道4选1的选择题,某考生心存侥幸,试图用抽签的方法给出答案,试求下列事件的概率: (1)恰有3题回答正确; (2)无一回答正确; (3)至少有1题回答正确。
单选题
20填空 设随机变量 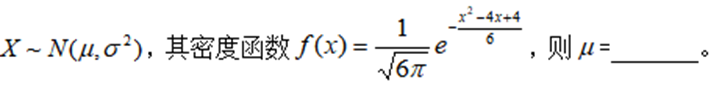
单选题
19填空 随机变量X的概率密度函数
单选题
18填空 随机变量X的数学期望
单选题
17填空 某射手对目标独立射击四次,至少命中一次的概率为
单选题
16填空 设随机变量X服从[0,2]上均匀分布,则 
单选题
15判断 事件A与B相互独立,则 
单选题
14判断 设A,B,C为同一试验的三个事件,则事件ABC表示A、B、C至少有一个发生。










