相关题目
23.j14 (2x + 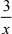 )dx 解:
)dx 解:
= [x2 + 3ln x]null
= 42 + 3ln 4 - (1+ 3ln1)
= 15+ 3ln 4
= 15+ 6 ln 2
22.j03 sin xdx
解:
= [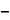 cos x]
cos x]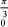
=  cos
cos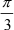
 (
( cos 0)
cos 0)
= 
 + 0 1
+ 0 1
= 2
21.j01 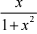 dx 解:
dx 解:
= 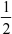 j01
j01 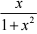 d(x2 + 1)
d(x2 + 1)= ( 1 ) ln
 x2 + 11
x2 + 11
= 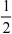 [ln(1+ 1)
[ln(1+ 1)  ln(0 + 1)]
ln(0 + 1)]
= 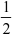 ln 2
ln 2
20.j04 tan2 xdx 解:
= j04 (sec2 x  1)dx
1)dx
= [tan x 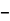 x]
x]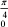
= 1 
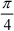
19.j( ) ( )
( )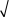 1 d一null 一 1
1 d一null 一 1
解:
令  1
1  x = t ,x = 1
x = t ,x = 1 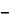 t2,dx =
t2,dx =  2tdt
2tdt
= (j)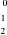
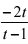 dt = 2j0
dt = 2j0 (1 +
(1 + 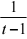 )dt
)dt
= 1  2 ln 2
2 ln 2
18.jnull4xe2xdx 解:
= 
 4j01 xd (e2x )
4j01 xd (e2x )
= [2x . e2x ]null 一 2j01 e2xdx
= 2e2 一 j01 e2xd (2x)
= 2e2 一 [e2x ]null
= e2 + 1
17.j01 x2 null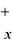 2一 2 dx 解:
2一 2 dx 解:
= j01 (x 一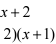 dx
dx
= 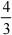 j01 x 1一 2 dx 一
j01 x 1一 2 dx 一  j01
j01 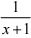 dx
dx
= 一  ln 2
ln 2
16.计算j
 dx .
dx .
解:
=  j04 (1一
j04 (1一  ) dx
) dx
=  j04 dx 一
j04 dx 一  j04 11nullnullin2nnulldx
j04 11nullnullin2nnulldx
= +  一 2 4
一 2 4
15.求定积分j nullx ln(1 + x)dx
解: =
= 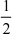 x2 [ln(x + 1)]null 一 j01
x2 [ln(x + 1)]null 一 j01  x2 .
x2 . 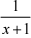 dx
dx
令t = 1+ x ,t = (1,2),dx = d (t 一 1) = dt
= 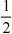 ln 2 一
ln 2 一 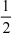 j12 (t null1)2 dt 1
j12 (t null1)2 dt 1
= 4
14.求定积分j null xe-2xdx
解:
=  -
- 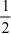 xe-2x +
xe-2x + 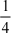 e-2x
e-2x  null
null
= - 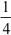 (
( + 1)
+ 1)










