单选题
29. 顶点在 x 轴上,两顶点的距离是 8,焦点距离是 10 的双曲线标准方程是( )
29. 顶点在 x 轴上,两顶点的距离是 8,焦点距离是 10 的双曲线标准方程是( ) 
A
A
B
B
C
C
D
D
答案解析
正确答案:A
解析:
首先,我们来看一下双曲线的标准方程是什么样子的。双曲线的标准方程是$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$,其中$a$表示顶点到中心的距离,$c$表示焦点到中心的距离,$b$通过勾股定理$b^2=a^2+c^2$来计算。
根据题目中给出的信息,顶点在$x$轴上,两顶点的距离是8,焦点距离是10。因为顶点在$x$轴上,所以$a$就是顶点到中心的距离,即$a=4$。又因为焦点距离是10,所以$c=5$。根据$b^2=a^2+c^2$,我们可以计算出$b=\sqrt{a^2+c^2}=\sqrt{4^2+5^2}=\sqrt{41}$。
所以双曲线的标准方程就是$\frac{x^2}{16}-\frac{y^2}{41}=1$,选项A是正确答案。
为了更好地理解双曲线,我们可以想象一下双曲线是两个不断向外扩张的弧线,类似于两个张开的喇叭口。焦点是双曲线的特殊点,是两个弧线的中心,顶点则是双曲线的起点。希望这个生动的比喻可以帮助你更好地理解双曲线的性质和特点。如果有任何疑问,欢迎继续提问哦!




 ( )
( )
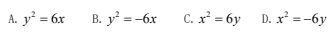
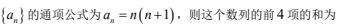 为( )
为( )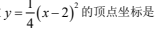 ( )
( )
 ( )
( )
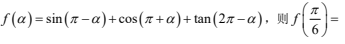 ( )
( )
 ( )
( )
 ( )
( )
 ( )
( )






