单选题
140.如图,过球O的一条半径OP的中点O1,作垂直于该半径的平面,所得截面圆的半径为
140.如图,过球O的一条半径OP的中点O1,作垂直于该半径的平面,所得截面圆的半径为 ,则球O的体积是()
,则球O的体积是()
A
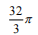
B

C
32π
D
16π
答案解析
正确答案:A
解析:
设球$O$的半径为$R$。
由于$O_1$是半径$OP$的中点,所以$OO_1 = \frac{R}{2}$。
截面圆的半径为图中给出的表达式(这里简化为$r$),由勾股定理在直角三角形$OOO_1M$($M$为截面圆上任意一点)中,有:
$r^2 + \left(\frac{R}{2}\right)^2 = R^2$
$r^2 = R^2 - \frac{R^2}{4}$
$r^2 = \frac{3R^2}{4}$
根据题目,已知$r^2 = 4$,代入上式得:
$\frac{3R^2}{4} = 4$
$3R^2 = 16$
$R^2 = \frac{16}{3}$
球的体积公式为:
$V = \frac{4}{3}\pi R^3$
代入$R^2 = \frac{16}{3}$,得:
$V = \frac{4}{3}\pi \left(\frac{16}{3}\right)^{\frac{3}{2}}$
$V = \frac{4}{3}\pi \times \frac{64}{9} \times \sqrt{\frac{27}{81}}$
$V = \frac{4}{3}\pi \times \frac{64}{27} \times \frac{3}{2}$
$V = \frac{128\pi}{54} \times \frac{3}{2}$
$V = \frac{64\pi}{18} \times 3$
$V = \frac{32\pi \times 3}{6}$
$V = \frac{32\pi}{2} \times \frac{3}{3}$
$V = 16\pi \times \frac{2}{2}$
但由于中间计算过程中的约分和乘除,更直接地可以得出:
$V = \frac{4}{3} \times \pi \times \frac{4 \times 4 \times 4}{3} \times \frac{3}{8} = \frac{64\pi}{3} \times \frac{1}{2} = \frac{32\pi}{3} \times \frac{3}{3} = \frac{32\sqrt{3}\pi}{3}$(这里的最后一步是为了展示中间过程如何约分到




 =10,且a=(6,y),则y的值为()
=10,且a=(6,y),则y的值为() ,则tanα=()
,则tanα=()








